General · Language · Media

What the heck is superposition?

John Healy

[Preliminary – requires clarification of the distinction between classical superposition (as for mechanical waves) and superposition that occurs in quantum mechanics (quantum superposition).]

Linear superposition of waves
John Healy using Apple’s Grapher

The linear venue

Some grocery stores still have spring scales in the fresh produce section. Let’s say, just to get the raw weight, you use the scale to weigh some oranges – 2 lb 6 oz. Then you weigh some apples – 3 lb 5 oz. Putting them together in a plastic bag from a nearby dispenser, you check the combined weight. The scale shows 5 lb 11 oz. A linear model, you see.

Imagine rigging an elastic string (or thin elastic cord) horizontally between two poles (like a long clothes line). First, you hang a small weight (which may be released remotely) from the center of the span. Then setup your smartphone camera for super slo-mo, start recording, and release the weight. Second, you hang together that weight and an identical one, and slo-mo again. How does the motion of the string in each case compare?

In high school, I built a small water tank (containing a water tunnel) to analyze the relative performance of foils for hydrofoils. Various shapes. It also might have been useful to model how waves interact (interfere) and combine (overlap). With waves originating from one or both ends of the tank, and demonstrating the principle of superposition – and the related mathematics. [1]

In particular, the mathematics of linearity – systems of linear equations, which came later in college. But those mathematics classes did not connect with my experience in fluid dynamics courses. (My recollection is that the professor for linear algebra did research in traffic analysis.)

As noted in a recent video (below) by Parth G, “Luckily, the universe seems to behave linearly very often …” That is, our linear mathematical models accurately predict the interactions of waves – in systems which are wave-like.

Wiki: “… many physical systems can be modeled as linear systems.” [2]

The wave equation – natural things and strings

• Wiki > Wave equation

The wave equation is a second-order linear partial differential equation for the description of waves – as they occur in classical physics – such as mechanical waves (e.g. water waves, sound waves and seismic waves) or light waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics.

Historically, the problem of a vibrating string such as that of a musical instrument was studied by Jean le Rond d’Alembert, Leonhard Euler, Daniel Bernoulli, and Joseph-Louis Lagrange.

Note that differentiability – as in a linear partial differential equation – assumes a continuous model space. Smoothness. (As in calculus for those infinitesimals.)

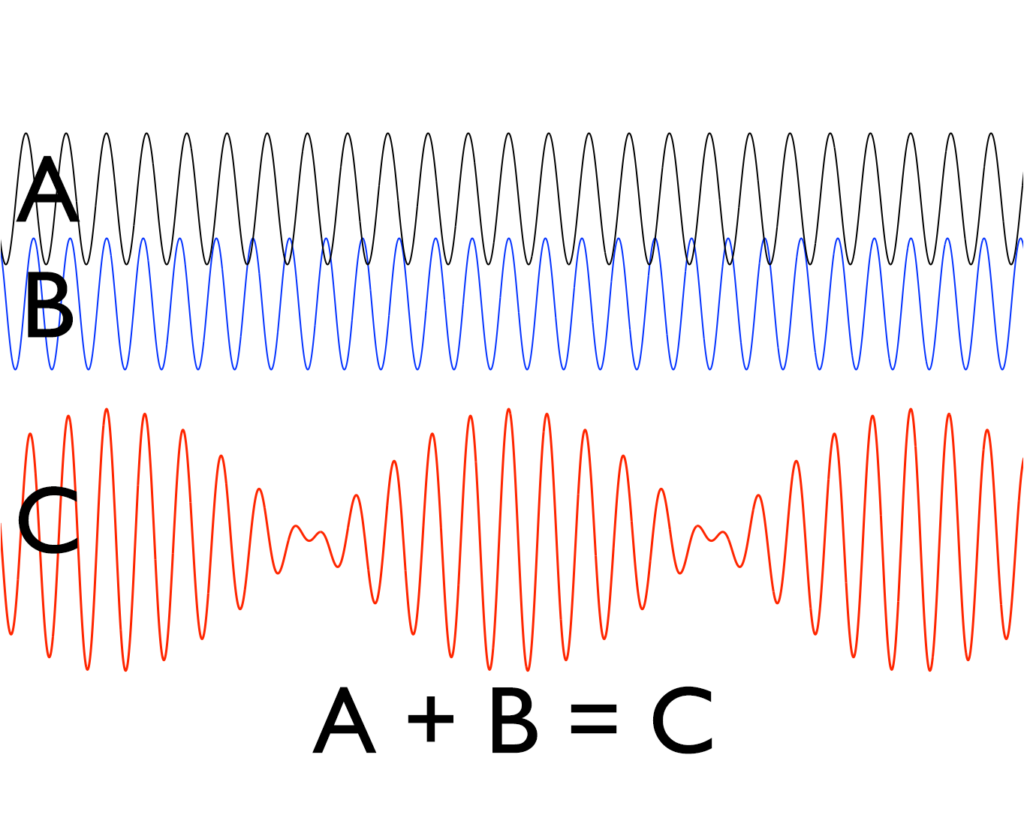
The superposition principle – for linear systems

Wiki has some animations here.

The math: “… if input A produces response X and input B produces response Y then input (A + B) produces response (X + Y).”

Additivity: F(x1 + x2) = F(x1) + F(x2)
Homogeneity: F(ax) = aF(x)

• Wiki > Superposition principle

The superposition principle, also known as superposition property, states that, for all linear systems, the net response caused by two or more stimuli is the sum of the responses that would have been caused by each stimulus individually.

A technical overview by a science communicator

Here’s another video by [Patreon] science communicator Parth G on a foundational mathematical concept in physics, both in classical and quantum physics. An introduction to the principle of superposition for waves, waves which can be modeled as (differential) linear equations.

• YouTube > Parth G > “How Waves Overlap, and Why Common Sense Works! Principle of Superposition for Linear Equations” (Nov 25, 2021)

… why does it make sense to add the displacement of each wave at every point in space and time in order to find the resultant wave? …

In this video, we will look at the Principle of Superposition. It explains why when two waves overlap, we can simply add their displacements at each point to find the resultant wave. This is what we would find reasonable due to our common sense. But common sense isn’t always correct – so why is it accurate here?

To understand this, we need to realize that the wave equation (the classical governing equation for describing all sorts of waves) is linear in wave displacement. In other words, the displacement of a wave (u) only appears as a single factor of u everywhere in the equation. … This linearity ensures that if we take any two known solutions of the wave equation, then adding them together produces yet another solution to the wave equation – in this case the resultant wave. …

Luckily, the universe seems to behave linearly very often, and any linear system can use the principle of superposition to find solutions that are formed by summing other existing solutions. …

Notes

[1] So, perhaps an earlier exposure to Fourier-transforms. And later a better understanding of Maxwell’s equations and the Schrödinger equation.

[2] With the caveat that: “Because physical systems are generally only approximately linear, the superposition principle is only an approximation of the true physical behavior.”

7 thoughts on “What the heck is superposition?”

  1. Additional note (2-8-2022): Clarification may be required for the distinction between classical superposition (as for mechanical waves) and superposition that occurs in quantum mechanics. Such a distinction is noted in Wiki’s article for the superposition principle, as well as Wiki’s article on Quantum superposition.

    … on the topic of quantum superposition, Kramers writes: “The principle of [quantum] superposition … has no analogy in classical physics.” According to Dirac: “the superposition that occurs in quantum mechanics is of an essentially different nature from any occurring in the classical theory.”

    When this article (below) talks about “light is in a superposition of … different polarized states,” the light in question is ambient light or beams of light vs. individual photons. While a single electron’s spin can be in a superposition of ‘up and ‘down,’ it’s not clearly stated that a single photon’s polarization can be in such a (quantum) superposition.[1]

    SUPERPOSITION AND SUNGLASSES

    • Wiki: “Many of the implications of the mathematical machinery [of quantum mechanics] are easily verified experimentally. In fact, many of the experiments can be performed with polaroid sunglass lenses.”

    • Caltech > Science Exchange > Topics > Quantum Science and Technology > Superposition > “What Is Superposition and Why Is It Important?” (2022)

    Concept

    Imagine touching the surface of a pond at two different points at the same time. Waves [of water] would spread outward from each point, eventually overlapping to form a more complex pattern. This is a superposition of [classical] waves. Similarly, in quantum science, objects such as electrons and photons have wavelike properties that can combine and become what is called superposed [superposition of mathematical quantum waves].

    Equations

    In mathematical terms, superposition can be thought of as an equation that has more than one solution. When we solve x^2 = 4, x can either be 2 or –2. Both answers are correct. Superposed wave functions will be more complicated to solve, but they can be approached with the same mindset.

    Observations

    … light is in a superposition of … different polarized states. … Superposition becomes apparent when we arrange more than one [polarizing] filter in different ways to tease out additional properties of light.

    As light waves interact with their surroundings, their properties change. Light that reflects off of the surface of a lake or snow-covered ground will be more likely to be polarized horizontally. If this light then encounters a filter that permits only vertically polarized light to pass through, the reflection will be blocked. This is how polarized sunglasses filter out the glare from reflective surfaces on a bright day.

    Notes

    [1] Superposition of a (single) photon’s polarization – a quantum state which is neither strictly (100%) horizontally or vertically polarized – is inferred from two examples of multiple polarizing filters.

    A. Two filters: a horizontal filter and a second rotated horizontal filter.

    B. Three filters: horizontal, diagonal, vertical.

    The “reset” of the superposition noted in case B is similar to what happens (“a clean slate”) to the superposition of an electron’s spin for three linked Stern–Gerlach apparatuses.

  2. Demo: “Polarized lenses are demonstrated, linearly polarizing light and showing the effect of orientation of a second lens.”

    • YouTube > Caltech’s Feynman Lecture Hall > Demo 21001: Polarized Filters – Demos: Polarized Filters and Quarter-Wave Plate (Nov 20, 2019)

    Incandescent light in unpolarized. By passing it through a polarizing lens, we pull out the components of the light that are parallel to the polarization axis. We can then examine the behavior of linearly polarized light as it is sent through additional filters.

    See 21001 in this list.

  3. I like this visualization (below) regarding superposition.

    • Phys.org > “Quantum physics in proteins: AI affords unprecedented insights into how biomolecules work” by Deutsches Elektronen-Synchrotron (11-3-2021)

    Quantum wave packet between two layers

    (caption) Illustration of a quantum wave packet in close vicinity of a conical intersection between two potential energy surfaces. The wave packet represents the collective motion of multiple atoms in the photoactive yellow protein. A part of the wave packet moves through the intersection from one potential energy surface to the other, while the another part remains on the top surface, leading to a superposition of quantum states. Credit: DESY, Niels Breckwoldt

  4. An interesting scenario regarding the wave function as verity.

    • Quanta Magazine > “Puzzling Quantum Scenario Appears Not to Conserve Energy” by Katie McCormick, Contributing Writer (May 16, 2022) – Superoscillation presents a paradox about conservation of energy for light in a box?

    As John Wheeler once said, “No progress without a paradox!”

    (In grad school, similar to my consideration of paradox as an insightful marker, eh.)

    In quantum mechanics, a particle is described by a wave function, … Wave functions can be expressed as sums [superpositions?] of sine waves, just as other waves can.

    Popescu, Aharonov and Rohrlich exposed the paradox using a thought experiment. Suppose you have a photon trapped inside a box, and this photon’s wave function has a superoscillatory region. Quickly put [without doing any work?] a mirror in the photon’s path right where [it is known that] the wave function superoscillates [how, in principle, might this be done, considering that such targeting requires energy?], keeping the mirror there for a short time. If the photon happens to be close enough to the mirror during that time, the mirror will bounce the photon out of the box.

    Remember we’re dealing with the photon’s wave function here. Since the bounce doesn’t constitute a measurement, the wave function doesn’t collapse. Instead, it splits in two: Most of the wave function remains in the box, but the small, rapidly oscillating piece near where the mirror was inserted leaves the box and heads toward the detector.

    Because this superoscillatory piece has been plucked [statistically or individually?] from the rest of the wave function, it is now identical to a photon of much higher energy. When this piece hits the detector, the entire wave function collapses. When it does, there’s a small but real chance that the detector will register a high-energy photon. It’s like the gamma ray emerging from a box of red light.

    Entangled verse

  5. Quantum superposition potentially improves the efficiency of photosynthesis or photovoltaic systems.

    What’s a light trap? (Vs. Optical tweezer.) This trap uses superposition so that all the photons are absorbed – no light is lost (due to the trap’s partially transparent mirror) – in a thin absorber.

    • Phys.org > “Physicists develop a perfect light trap” by Vienna University of Technology (August 25, 2022) – “In many technical applications, you only have a thin layer of material available and you want the light to be absorbed exactly in this layer.” (Prof. Stefan Rotter, Institute of Theoretical Physics at TU Wien)

    Whether in photosynthesis or in a photovoltaic system: if you want to use light efficiently, you have to absorb it as completely as possible. However, this is difficult if the absorption is to take place in a thin layer of material that normally lets a large part of the light pass through.

    “The system has to be tuned exactly to the wavelength you want to absorb,” says Stefan Rotter.

    Light trap for thin absorber
    Credit: TU Wien

    Related articles

    • Phys,org > “What color is a mirror? Explaining mirrors and how they work” by Jacob Livesay (July 5, 2022)

  6. Question: Is superposition and interference the same?

    • openstax > Wave Interaction: Superposition and Interference – “The two special cases of superposition that produce the simplest results are pure constructive interference and pure destructive interference.”

    (quote) While pure constructive interference and pure destructive interference can occur, they are not very common because they require precisely aligned identical waves. The superposition of most waves that we see in nature produces a combination of constructive and destructive interferences. [OpenStax is part of Rice University, which is a 501(c)(3) nonprofit.]

    • Wiki > Superposition principle > Wave interference

    (quote – noted previously) There are some likenesses between the superposition presented in the main on this page and the quantum superposition. Nevertheless, on the topic of quantum superposition, Kramers writes: “The principle of [quantum] superposition … has no analogy in classical physics.” According to Dirac: “the superposition that occurs in quantum mechanics is of an essentially different nature from any occurring in the classical theory [italics in original].”

    Quantum interference
    R. P. Rundle, P. W. Mills, Todd Tilma, J. H. Samson, and M. J. Everitt, CC by 3.0, via Wikimedia Commons

  7. So, what about non-linear systems?

    This article highlights non-linearity in new, more detailed supercomputer simulations of black hole mergers “that have been routinely observed by LIGO (Laser Interferometer Gravitational-wave Observatory).”

    • Caltech > News > “Physicists Create New Model of Ringing Black Holes” by Whitney Clavin (February 21, 2023) – New analysis shows “nonlinear” effects contained in gravitational waves.

    “Nonlinear effects are what happens when waves on the beach crest and crash” says Keefe Mitman, a Caltech graduate student who works with Saul Teukolsky (PhD ’74), the Robinson Professor of Theoretical Astrophysics at Caltech with a joint appointment at Cornell University. “The waves interact and influence each other rather than ride along by themselves. With something as violent as a black hole merger, we expected these effects but had not seen them in our models until now. New methods for extracting the waveforms from our simulations have made it possible to see the nonlinearities.”

Comments are closed.