[Draft]

A recent Nature article (below) was inspiration for this post. I’ve been encountering the use of topology in physics for some time. Typically the mathematics is elusive, but the notions are compelling.

Wiki > Topology

A continuous deformation (a type of homeomorphism) of a mug into a doughnut (torus) and a cow into a sphere.

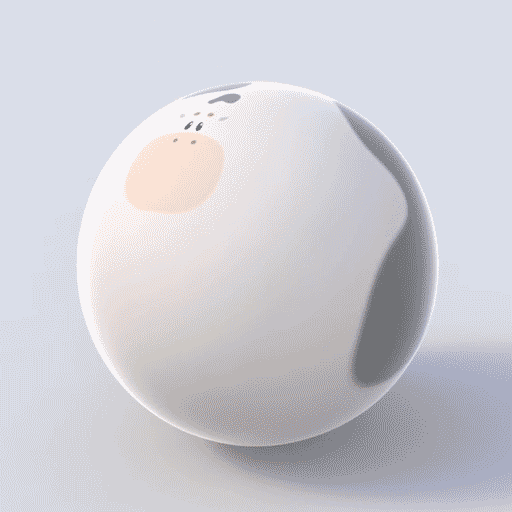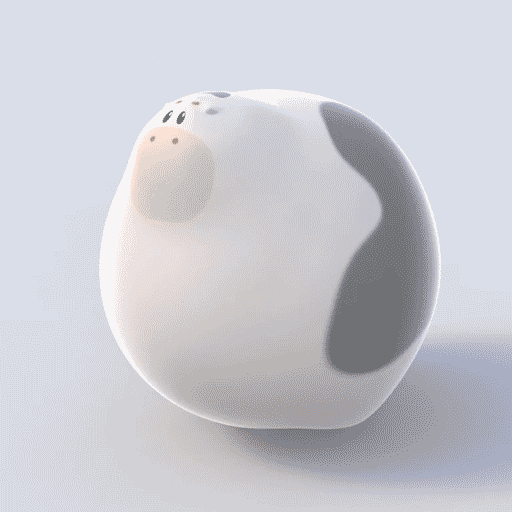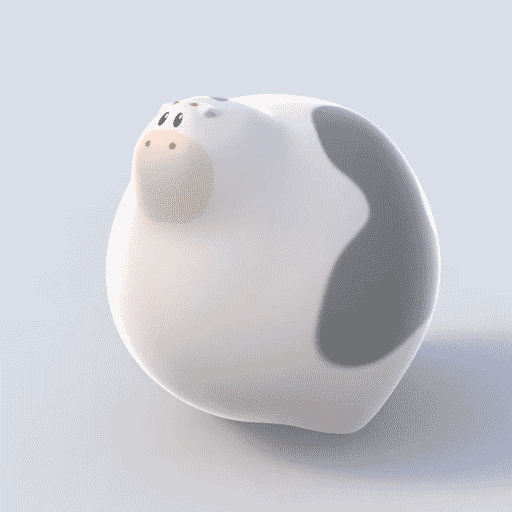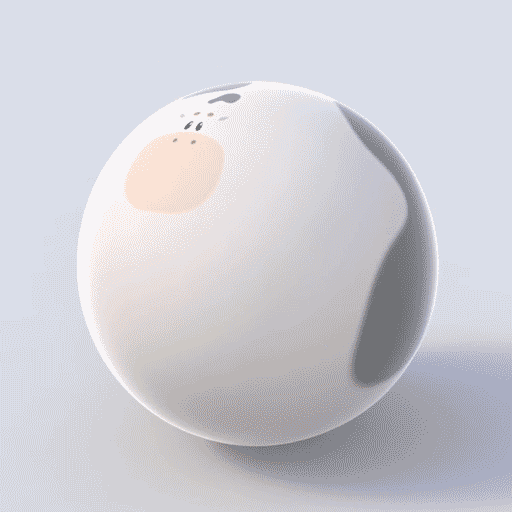
In mathematics, topology … is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling and bending, but not tearing or gluing.

Intuitively, two spaces are homeomorphic if one can be deformed into the other without cutting or gluing. A traditional joke is that a topologist cannot distinguish a coffee mug from a doughnut, since a sufficiently pliable doughnut could be reshaped to a coffee cup by creating a dimple and progressively enlarging it, while shrinking the hole into a handle.

Homeomorphism can be considered the most basic topological equivalence. Another is homotopy equivalence. This is harder to describe without getting technical, but the essential notion is that two objects are homotopy equivalent if they both result from “squishing” some larger object.

Topology is relevant to physics in areas such as condensed matter physics, quantum field theory and physical cosmology.

A topological quantum field theory (or topological field theory or TQFT) is a quantum field theory that computes topological invariants.
Although TQFTs were invented by physicists, they are also of mathematical interest, being related to, among other things, knot theory, the theory of four-manifolds in algebraic topology, and to the theory of moduli spaces in algebraic geometry.

The topological classification of Calabi-Yau manifolds has important implications in string theory, as different manifolds can sustain different kinds of strings.

In cosmology, topology can be used to describe the overall shape of the universe. This area of research is commonly known as spacetime topology.

Nature > News Q&A > “The mathematician who helped to reshape physics” by Davide Castelvecchi (August 4, 2020) – Barry Simon [who is at the California Institute of Technology in Pasadena] linked a phenomenon that had shocked physicists to topology, the branch of mathematics that studies shapes.

In recent years, physics has been swept by ideas from a branch of mathematics called topology. Topology is the study of objects that deform continuously without tearing, for example through stretching or twisting. But it is now proving crucial to understanding the shapes of quantum waves formed by the electrons inside matter. These waves can form shapes such as vortices, knots and braids that give materials a variety of exotic properties. In 1983, Barry Simon was the first person to make the link between strange phenomena in materials and topology.

German physicist Klaus von Klitzing won a Nobel prize for the [Hall] effect’s discovery in 1985. But it took several breakthroughs by theoretical physicists to begin to understand the phenomenon. And it took Simon — a mathematical physicist who uses mathematical tools to solve theoretical problems that emerge from nature — alongside collaborators, to recognize that equations created to describe the quantum Hall effect were a manifestation of topology. It was topology that was making the material’s resistance robust to small changes, allowing it to change in only discrete jumps [due to the topological effect, called a winding number].