How dark is the universe – optically?
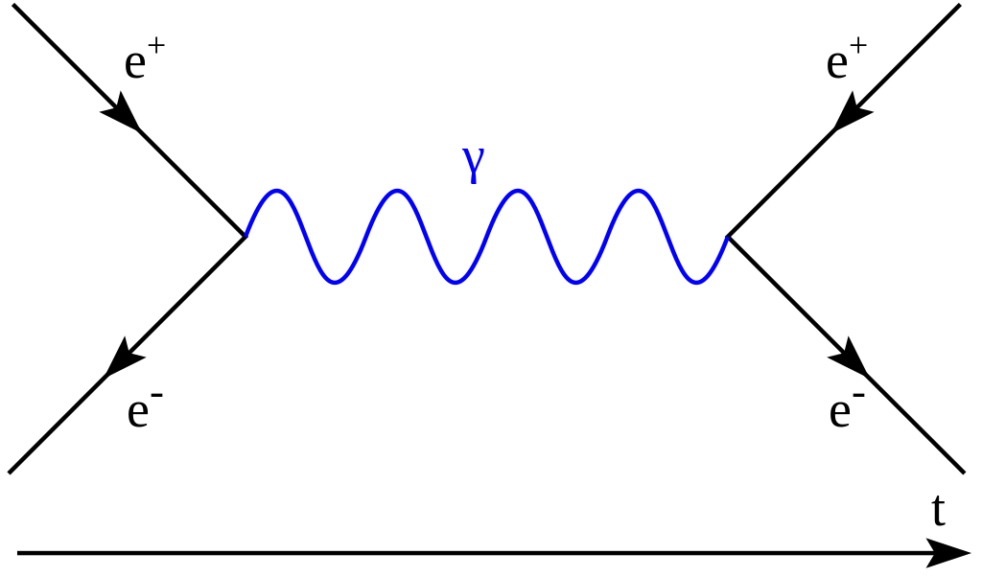
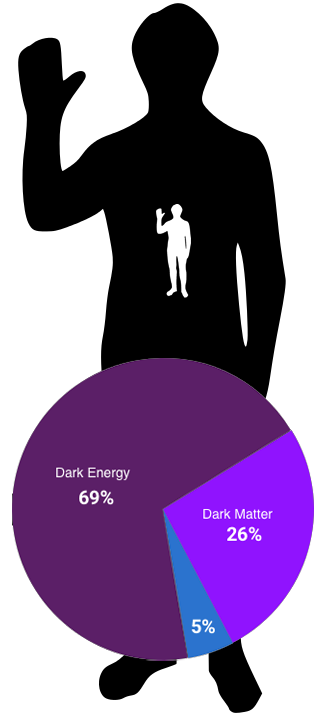
How dark is the universe? Optically – for visible light. Far away from star light and reflected dust. Here’s an interesting perspective on electromagnetic (EM) cosmic energy density – just for optical wavelengths. And without any clarification of fuzzy bounds for a galaxy’s reach. The entire electromagnetic spectrum is another story. • Live Science >… Continue reading How dark is the universe – optically?