[Preliminary 11-11-2023] [“Quantum foundations” series]
Table of contents
- Context
- First big idea: wave function
- Second big idea: wave function as sum of sines and cosines
- Third big idea: Fourier transform
- Fourth big idea: momentum of a wave depends on its wavelength
- macOS Grapher examples
- Conclusion
- Lincoln’s (Fermilab) video
- Notes
- Related posts
Context
This post was inspired by Don Lincoln’s latest YouTube video (below).
Insights from quantum field theory (QFT) have helped me better understand strange aspects of quantum theory [1].
In particular, leaving behind notions of point particles and wave-particle duality, and just going with fields and wavepackets in those fields (and their interactions). As Don Lincoln noted, “It’s perfectly reasonable to think of fundamental particles as wavepackets.“
Wavepackets are superpositions of multiple frequencies (excitations, vibrations). Inherently superpositions. Mathematicaly, this amounts to Fourier transforms.
Wiki > If the packet is strongly localized, more frequencies are needed to allow the constructive superposition in the region of localization and destructive superposition outside the region.
So, Fermilab’s Don Lincoln’s latest YouTube video on the uncertainty principle caught my attention. Lincoln explains that the foundation of that principle predates Heisenberg’s formulation (1927) – grounded in the mathematics of Fourier (1807).
If you know where an electron is [its position], you have no idea how fast [its momentum] or even if it’s moving. That’s the gist.
It’s simple really. All it really says is that if you measure one variable well, you will measure the other one poorly. You can’t simultaneously measure both well.
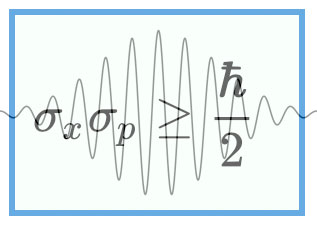
First big idea: In quantum mechanics, everything is governed by a thing called a wave function. A wave function tells you where a particle can be, and it has a range of possible locations that’s called Delta x.
Basically, where the wave function – actually the square of the wave function – is large, the particle is likely to be there. Conversely, where the square of the wave function is zero, the particle can’t be there at all. The width of the [squared] wave function gives you a sense of the range of possible locations where the particle can be, which is a way of saying the width is a measure of your uncertainty of the position of the particle.
Second big idea: we can create any wave function using a sum (series) of sines and cosines.
Okay. So, what was Fourier’s insight? Basically, he realized that for any function that you can build it by adding together the right amounts of sine and cosine waves.
He begins with an example of how a square wave can be mathematically constructed by superimposing multiple sine waves of specific frequencies. Approximated as closely as desired (see my example below).
There likely are no true square waves in nature. Likewise fundamental so-called particles are not singular waveforms (single-mode plane vibrations) either.
Third big idea: Fourier transforms show that the range of locations (Delta x) and the range of waves are connected.
Lincoln uses some visuals to make the connection between two graphs:
- the position space plot – of the square wave, with position on the x axis
- a W space plot – with the number of wiggles on the x axis (how many different sine waves are added and how much amplitude each one contributes to the function series)
The information in a wave function series can be represented in two “spaces” and transformed from one to the other.
The x-axis of this second plot is kind of funny. It is basically the number of wiggles – the number of wavelengths – in a fixed distance. There was one, then three, then five, and so on.
For the purposes of this video, I’m going to write the number of wiggles as W, and it equals one over the wavelength. Wavelength is written as the Greek letter lambda. Shorter wavelength means higher W – that’s how it works.
So, now I need to make a super important point. These two graphs … represent exactly the same information. The two plots are effectively the same thing, but one records the shape of the function in position space, while the other records the number and amount of waves, which we might call the function in W space.
Lincoln then uses the normal distribution (aka bell curve) – vs. the square wave – as a more realistic function to advance his demonstration: “We can do a Fourier transform and find out what the shape of the curve will be in W space.”
It turns out that the Fourier transform of a normal distribution is also a normal distribution.
Now here is the most important point. It turns out that the width of the normal distribution in W space is related to the width of the normal distribution position or x space. So, if you do the math, you find that Delta x times Delta W is equal to one over two times pi.
𝜟x𝜟W = 1/2π
So, what does that mean? It means that if Delta x gets small, then Delta W gets big and vice versa. They can’t both be small at the same time.
Fourth big idea: The momentum of a wave depends on its wavelength.
Lincoln then recaps some history in quantum mechanics: Louis De Broglie (1924) proposed that the momentum (p) of a wave = h/𝞴. So:
p = hW
𝜟p = h𝜟W or 𝜟p/h = 𝜟W
So, from above 𝜟x𝜟W = 𝜟x𝜟p/h = 1/2π or 𝜟x𝜟p = h/2π = h_bar
So, this looks a lot like the Heisenberg Uncertainty Principle, although it’s missing that one-half factor, which means that I haven’t derived the uncertainty principle here. It turns out that derivation is a little more complicated …
macOS Grapher examples
• Square wave Fourier series (movie)

• Gaussian 3D wavepacket (movie)
Conclusion
So, from the four big ideas, Lincoln concludes, “you have everything you need to see where the Heisenberg Uncertainty Principle comes from.“
Well, hmm, … So, I’d still like to see a realistic visualization of how a photon – as a wavepacket – results from an electron’s transition from a higher to lower energy state (whether that resolves the quantum topology or not):
An example which models how a spacetime modal transition in energy (a process which is not instantaneous) entails a superposition of many waves into a wavepacket – a sum of subtle frequency and/or phase differences, with constructive superposition in the region of localization and destructive superposition outside the region.
At that point, it’s reasonable that a superposition (extended in space) is connected to the Uncertainty Principle, because that sum of waves inherently has no single position or momentum – only a range. It’s a composite only characterizable by relational field interactions. And standard deviations.
Perhaps there’s a taste of this model with the Hydrogen spectral series and the 21 cm fine and hyperfine emission lines due to “spreading” from local field interactions and relativistic effects.
Anyway, a visualization in macOS Grapher is TBD, after looking at:
• Wiki > Uncertainty principle > Visualization and Wave mechanics interpretation
Adding together all of these plane waves comes at a cost, namely the momentum has become less precise, having become a mixture of waves of many different momenta.
Lincoln’s video
• YouTube > Fermilab > “Demystifying the Heisenberg Uncertainty Principle” by Don Lincoln (Oct 16, 2023)
Description
The Heisenberg Uncertainty Principle is one of the most non-intuitive concepts in all of quantum mechanics. It says that it is impossible to precisely know both an objects location and its motion. Know one well and you must know the other poorly. The origins of this are deeply tied to the wave nature of matter and the connection between waves and momentum. In this video, Fermilab’s Dr. Don Lincoln sorts it all out.
Fourier transform square wave:
https://mathworld.wolfram.com/FourierSeriesSquareWave.htmlFourier transform gaussian:
https://mathworld.wolfram.com/FourierTransformGaussian.htmlAdditional Fourier transform explainer:
https://mriquestions.com/fourier-transform-ft.htmlWavelength, momentum, and wave number:
http://faculty.chas.uni.edu/~shand/Mod_Phys_Lecture_Notes/Chap6_Matter_Waves_Notes_s12.pdf
Notes
[1] So, perhaps a series of “demystifying” articles, eh.
- Demystifying point particles
- Demystifying wave-particle duality
- Demystifying quantum spin
- Demystifying the uncertainty principle
- Demystifying force (charge, mass)
- Demystifying singularities
- TBD
