[“Quantum foundations” series]

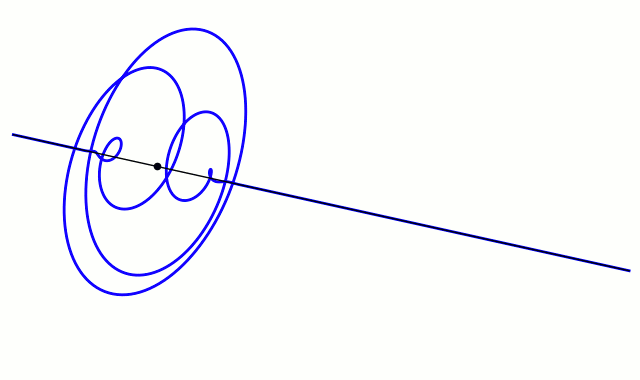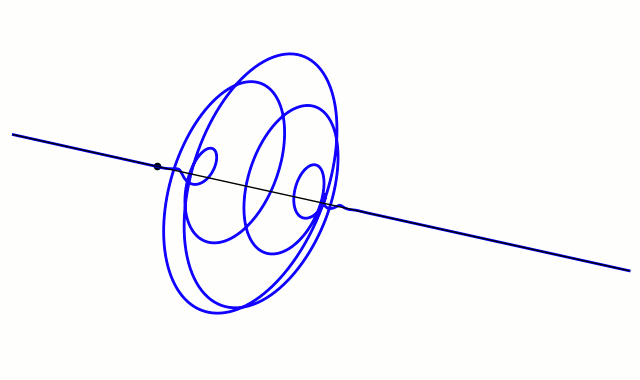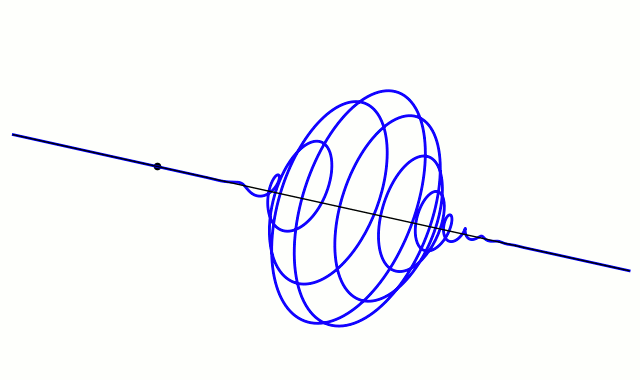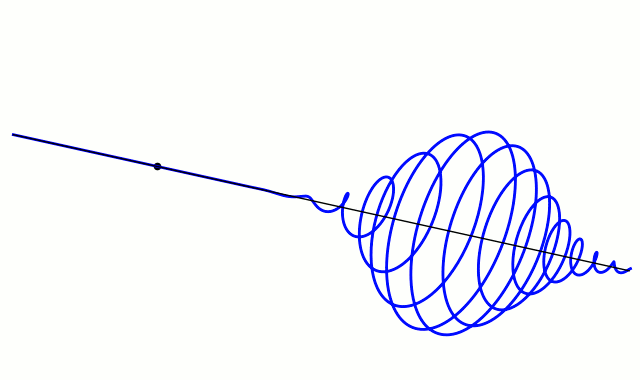
TABLE OF CONTENTS

1. Quantum field theory (QFT) landscape
2. Is QFT incomplete?
3. Light speed sans mass
4. The math of fields
5. Excitations in cosmic microwave background
6. Questions
7. Visualizing wave packets

QUANTUM FIELD THEORY (QFT) LANDSCAPE

Some recent articles prompted me to further explore (revisit once again, eh) some key features of quantum field theory (QFT). Without grasping all the esoteric math.

1. Understanding quantum field theory (QFT) as a grid-like model of dynamic fields in which excitations can be localized.

As noted in a prior post (“QFT – How many fields are there?“), not all physicists tally these fields in the same way.

2. Visualizing such localized excitations, that is, wave packets. How are these mathematically constructed (at least, in one or 2 dimensional graphs). Wave packets and superposition of waves.

How matter waves enter into superpositions and how this allows wave packets to form.

Generally, visualizing how sine (or cosine) waves add together. Since “the plane waves we add together will individually be solutions of the Schrödinger equation.”

3. Pondering that in a few fields these excitations move at light speed whereas excitations in the rest cannot. Due to the latter interacting (to varying degrees) with the Higgs field, according to the Standard Model.
4. Sidestepping the cosmic speed limit for such excitations – in particular situations. Because light speed varies with medium. For example, in water light speed is only 0.75 of that in the “empty” vacuum of space. [See separate post.]

And interactions in a non-dispersive vs. dispersive medium.

Cherenkov radiation is electromagnetic radiation emitted when a charged particle (such as an electron) passes through a dielectric medium at a speed greater than the phase velocity (speed of propagation of a wavefront in a medium) of light in that medium.

HOW IS QUANTUM FIELD THEORY INCOMPLETE?

As reported by Google’s Search Console each month, the most popular page on this blog is “QFT – How many fields are there?” Via Google searches like “how many quantum fields are there” or “list of quantum fields” or “how many fields are there in physics.”

Regarding so-called fundamental “objects” and fields, here’s how theoretical physicist David Tong tallies them (see article below).

There’s a quark field — in fact, there are six different quark fields throughout the universe. There are neutrino fields, there are fields for gluons and W bosons. And whenever we discover a new particle, the most recent being the Higgs boson, we know that associated to that is a field which underlies it, and the particles are just ripples of the field.

• Quanta Magazine > “What Is Quantum Field Theory and Why Is It Incomplete?” by Steven Strogatz (August 10, 2022) – A chat with theoretical physicist David Tong [University of Cambridge] about this enigmatic theory.

This Quanta Magazine article provides some historical recap for the notion of physical fields. For example, Michael Faraday’s work, and how “thin air” is not empty.

And in quantum mechanics, “if you start with a field, and you apply the rules of quantum mechanics, you end up with a particle.”

Then later, “How each of those fields [in the Standard Model] interacts with the others.”

[Tong] So there’s this sort of intricate dance between what particles are doing, and what fields are doing. And really, his [Faraday’s] big contribution was to say these fields are real, they’re really every bit as real as the particles.

So by the time quantum mechanics came around … there’s kind of a question that emerges, which is, how should you think of this relationship between the fields on the one hand and the photons on the other. And I think there’s two logical possibilities for the way this could work:

.1. It could be that you should think of electric and magnetic fields as comprised of lots and lots of photons, rather like a fluid is comprised of lots and lots of atoms, and you think the atoms are the fundamental object.

.2. Or alternatively, it could be the other way around, it could be that the fields are the fundamental thing. And the photons come from little ripples of the fields.

And the big development in, well, it sort of starts in 1927. But it takes a good 20 or 30 years until this is fully appreciated. The big appreciation, then, is that it’s the fields that are really fundamental, that the electric and magnetic field is at the basis of everything. And little ripples of the electric and magnetic field get turned into little bundles of energy that we then call photons due to the effects of quantum mechanics.

And the wonderful big step, one of the great unifying steps in, in the history of physics, is to understand that that same story holds for all other particles [in the Standard Model].

[Strogatz] … physicists tell us that at the deepest level, everything is made up of mysterious entities, fluid-like substances that we call quantum fields. These invisible fields sometimes act like particles, sometimes like waves [ahem]. They can interact with one another.

Tong enumerates the “16” fields (hmm):

• “Force fields” (3) – photon (electromagnetism), gluon, W or Z boson
• “Matter fields” (12 = 3 x 4) – electron, up quark, down quark, electron neutrino; mujon, strange quark, charm quark, muon neutrino; tau, top quark, bottom quark, tau neutrino
• Higgs

LIGHT SPEED SANS MASS

Regarding the Higgs, Tong provides an analogy, an admittedly “bad” one. Namely, that “it acts a little like treacle or molasses.”

The particles sort of have to push their way through this, this Higgs field to make any progress. And that sort of slows them down. They would naturally travel at the speed of light, and they get slowed down by the presence of this Higgs field. And that is responsible for the phenomenon that we call mass.

Yeah, a misleading analogy. It’s really “bad” – “it sort of suggests that there’s some friction force” with a dependency on “size” or “streamlining” of the (so-called) particle.

The 1993 “winning” analogy provided elsewhere on this blog is about interactions – an analogy to the degree of “popularity” (relational standing) of various “actors” moving through a throng. [1]

My description: A common metaphor is a dynamic tableau of people moving about a highly attended gala. Complete with fans, hangers-on, and paparazzi. Those with more celebrity experience higher resistance moving through the throng. Inconsequential attendees and incognitos move easily about with less interaction, less hinderance.

Even the equations (which Tong seeks to visualize) really are about field interactions and related energy fluctuations. As noted elsewhere, “Energy is not a real thing, but rather a way to keep track of different interactions.” Which is something Tong does mention about proton or neutron “mass” – that “what’s going on inside the proton or neutron (wild fluctuations of quantum fields) [gives] them their mass” [vs. the 0.1% from quarks].

And Strogatz then notes that strong, confined interactions “are associated with some large amount of energy” which entails inertia (mass).

THE MATH OF FIELDS

Their discussion touches on the complicated math of fields, the continuous nature of space and time, mathematical (lattice) models which discretize space and time. And finally, a connection with one of my favorite aspects of quantum theory, topology – as related to parity violation (handed-ness). [2]

And then the evolution of physics and math: “The kind of area of mathematics that this has been most useful in is ideas to do with geometry.” For example, Einstein’s theory of general relativity.

[Strogatz] … these fields that can, as you say, sniff out the contours, the valleys, the peaks, the wholes of surfaces of global objects.

EXCITATIONS IN COSMIC MICROWAVE BACKGROUND

Regarding the cosmic microwave background (CMB), Tong notes that:

The fluctuations that we see are fairly vanilla, they’re just those that you would get from free fields [just bouncing up and down like a harmonic oscillator]. … And it would be nice to see some non-Gaussianity, which will be telling us about the interactions between the fields back in the very, very early universe. … the Planck satellite has… taken a snapshot of the CMB in ever clearer detail, and the non-Gaussianities that are there, if there are any there at all, are just smaller than, than the Planck satellite can detect.

QUESTIONS

The interview ends with some open questions, such as:

Why is the Higgs so light? It’s also there with dark energy. Why is the cosmological acceleration of the universe so small compared to what we, we think it is.

VISUALIZING WAVE PACKETS

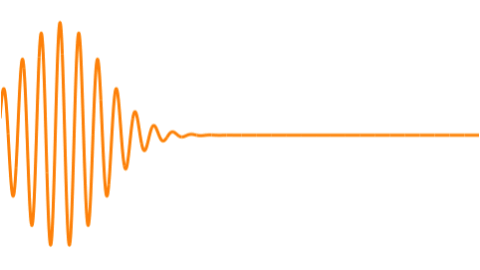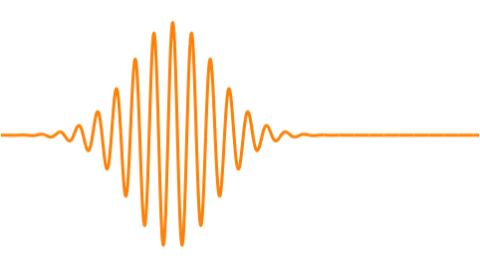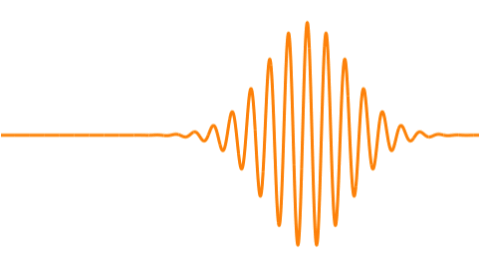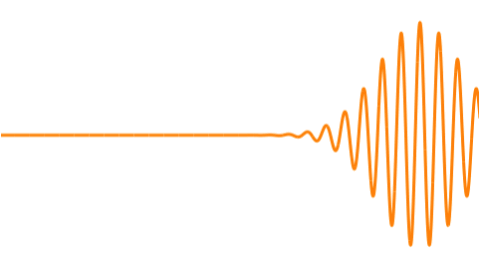
Recently I’ve also been using Apple’s Grapher app to better visualize wave interactions as superpositions of sine or cosine waves. [3] Also superpositions which represent traveling wave packets. Gaussian wave packets in classical / quantum mechanics. Mostly in 2D. Classroom physics. Interference and beats, etc. [4]

In a broader context of wave functions and Schrödinger’s equation.

Grapher examples

For non-dispersive medium. [5][6]

Click on an image for larger view.

So, combining (adding) two cosine waves of slightly different frequencies to create a wave beat is a common example. Straightforward.

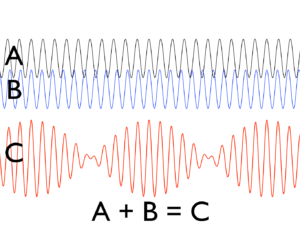
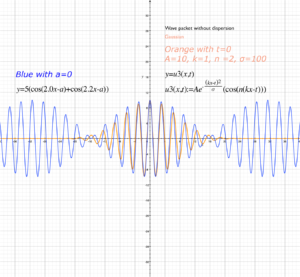
But I found that starting with a Gaussian “blip” and multiplying (modulating) that with a cosine produced the desired results as depicted in many references (including Wiki’s article on wave packets) – an “envelope of localized wave action that travels as a unit.”

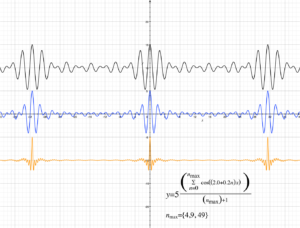
Combining a bunch of such cosine waves of slightly different frequencies gets a more defined wave-packet-like beat.

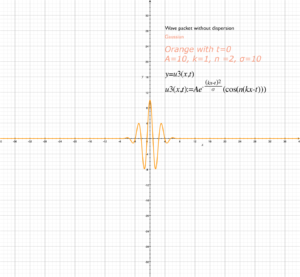
And adjusting the Gaussian’s width gets a sharper (narrower) wave packet.

Reference examples

Via search for “equation for wave packet in 2d”

• Physics classroom > Interference and beats

• The star garden > Schrödinger’s equation

re Leonhard Euler’s formula for e^ix = cos(x) + i sin(x)

• Wiki > Gaussian wave packets in quantum mechanics

re localization: If the packet is strongly localized, more frequencies are needed to allow the constructive superposition in the region of localization and destructive superposition outside the region.

• Phys.libretexts.org > Elementary stuff > wave packets and superposition

• Harvard.edu > Lecture > Wavepackets (via Searching for “equation for 1d wave packet width”)

Wavepacket simulator(s)

Software – an app or applet – which demonstarates how waves linearly add up to packets, something like this:

• The wavepacket simulator

Or here:

• Wave Packet JavaScript Application

Perhaps like this page but able to add more than 2 waves:

• Physics classroom > Wave Addition Interactive which has an iOS app (with $ add-ons)

Or here, online interactive for two pre-defined waves example:

• Geogebra.org > Addition of sine waves by E_Cami

Add two sine waves with different amplitudes, frequencies, and phase angles. What do you notice?

Add two sine waves with the same amplitude, frequency, and phase angle.

What do you notice?

— Change the frequency and see what happens;
— Change the phase angle and see what happens.

Add two sine waves with the same amplitude, frequency, and opposite phase angles. What do you notice?

Add two sine waves with the same amplitude and frequency, and with phase angles that differ by 180 degree. What do you notice?

A bunch here:

• Khadley.com … Colorado.edu > Physics 207 > Adding waves

This PhET Wave Interference simulation allows you to add waves together in real time. Please run this simulation and see how the signal changes as you vary the amplitude and frequency of the waves.

Or here for two sine waves, interactive:

• Academo.org > Wave Interference and Beat Frequency

Notes

[1] Which I prefer to view as something due to topological profiles of those excitations (“knots”) interacting with the quantum vacuum (or perhaps a scalar field like the Higgs – “the Higgs boson is the only particle that doesn’t spin”). In other words, even as Tong describes space and time as geometric objects, so-call point particles are geometric tangles in the “flow.”

In some sense, also an analogy of so-called quantum particles – localized field excitations – as the realized “notes” from plucking the “strings” of quantum fields. Akin to modal resonances of those fields (as confined or free).

[2] Tong makes an interesting connection between topology and quantum computing:

… one of the most powerful ways of building a quantum computer is to use topological ideas of quantum field theory, where information isn’t stored in a local point but it’s stored globally over a space. The benefit being that if you nudge it somewhere at a point, you don’t destroy the information because it’s not stored at one point. It’s stored everywhere at once.

[3] As well as locating some other online visualization tools via searching for “equation for wave packet in 2d.”

And reviewing some math like Leonhard Euler’s formula for e^ix = cos(x) + i sin(x).

• Wiki > Gaussian wave packets in quantum mechanics

And in particular, re localization, Wiki:

A wave packet is a localized disturbance that results from the sum of many different wave forms. If the packet is strongly localized, more frequencies are needed to allow the constructive superposition in the region of localization and destructive superposition outside the region.

[4] Trigonometry

The GMU page uses this Product-to-Sum Identity

cos α cos β = 1⁄2 [cos(α – β) + cos(α + β)]

or

A cos(α – β) + A cos(α + β) = 2A cos α cos β

which is noted here:

• Alamo Colleges District, San Antonio TX > Math

[5] Trigonometric identities also are referenced in Wiki > Dispersion (water waves)

Group velocity

Interference of two sinusoidal waves with slightly different wavelengths, but the same amplitude and propagation direction, results in a beat pattern, called a wave group. As can be seen in the animation, the group moves with a group velocity c[sub]g different from the phase velocity c[sub]p, due to frequency dispersion.

[6] Wave packet graphics

• GMU.edu > physics > Are there any monochromatic waves in nature?

There are no strictly monochromatic waves in nature. For example, the generating source of the wave may move slightly, introducing spurious frequencies.

From the point of view of sending information, these waves are not useful. They are the same throughout time and space. Something must therefore be modulated, such as frequency or amplitude, in order to convey information. The resulting wave may be a perturbation that acts over a short distance, i.e. a wave packet. This wave packet can be considered to be a superposition of a number of harmonic waves, in other words a Fourier series or integral.

In order to convey information, something more than a simple harmonic wave is needed. However, the superposition of many such waves of varying frequencies can result in an “envelope” wave and a carrier wave within the envelope. The envelope can transmit data. A simple example is the superposition of two harmonic waves with frequencies that are very close (w1 ~ w2) and of the same amplitude.

• Wiki > Wave packet

Image captions:

1. Propagation of a wave packet in a non-dispersive medium. We can see there is no difference between phase velocity and group velocity.
2. Propagation of a wave packet in a dispersive medium. We can see the difference between phase velocity and group velocity

In physics, a wave packet (or wave train) is a short “burst” or “envelope” of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet’s profile may remain constant (no dispersion) or it may change (dispersion) while propagating.

As discussed here also:

• Virginia > Physics > “Wave Equations, Wavepackets and Superposition by Michael Fowler, UVa 9/14/06” – a wave function is nonzero in a limited region of space.

Wavepackets and the Principle of Superposition

To return momentarily to the electron traveling through a vacuum, it is clear physically that it must have a wave function that goes to zero far away in either direction (we’ll still work in one dimension, for simplicity). A localized wave function of this type is called a “wavepacket”. We shall discover that a wavepacket can be constructed by adding plane waves together. Now, the plane waves we add together will individually be solutions of the Schrödinger equation.

The First Step in Building a Wavepacket: Adding Two Sine Waves

If we add together two sine waves with frequencies close together, we get beats. This pattern can be viewed as a string of wavepackets, and is useful for gaining an understanding of why the electron speed calculated from … above is apparently half what it should be.

This formula represents the phenomenon of beats between waves close in frequency [in phase at the origin]. The first term, sin (kx – wt ), oscillates at the average of the two frequencies. It is modulated by the slowly varying second term, often called the “envelope function“, which oscillates once over a spatial extent of order …. This is the distance over which waves initially in phase at the origin become completely out of phase. Of course, going a further distance of order …, the waves will become synchronized again.

Or here:

• Pitt.edu > “The Quantum Theory of Waves and Particles” by John D. Norton (2001 – 2022)

How matter waves enter into superpositions and how this allows wave packets to form.

How Heisenberg’s uncertainly principle places a limit of the definiteness of quantities.

The difference between uncertainty and indefiniteness.

What is quantum measurement (collapse of the wave packet).

How probabilities essentially enter into quantum theory and why this was initially regarded as a failure of causality.

Related posts

• Proton soup – a turbulent, dynamically complicated structure

• Evidence for new physics? > Fermilab’s Muon g-2 results announced

• Reality is fields