Happy Pi Day!

When you’re trying to solve any interesting problem (a problem about almost anything) — a problem with lots of interplay between different things, it’s important to know what’s important and not, what makes a big effect on the result and not. And just how precise the result needs to be anyway (at least if you’re a pragmatist). This is particularly important in modern physics because the equations are so complex — so complex that even computer simulations may not help much. [1]

So, the first stage is to carefully define the scope and domain of applicability of the problem. Mathematically, you look at the magnitude that each factor (or variable) contributes to the situation and impacts the result. You consider first order, second order, third order, etc., effects.

The trick, of course, is to be clever in selecting what matters (what can be ignored) in the first place — which is not always obvious. While I had been trained in the scientific method, my first wide exposure to this challenge was after grad school when I was a consultant at the Claremont Colleges computer center. My main role was to help grad students with their statistical analyses when they didn’t get the results that they expected — when they couldn’t “prove” (claim confidence about) something or there was no practical result [2].

Well, physicists have much the same challenge. Comprehensive equations can be way too messy mathematically and computationally impractical or too costly to solve. An essential problem solving strategy is simplification — solve a simpler or similar problem (or break into simpler problems or steps). [3] Simplifying the context or domain of applicability still might lead to acceptable (useful) results  and thereby simplify the equations.

This consideration is what makes the notion of effective theory so important in physics (among other disciplines). This is an important topic in Sean Carroll’s books and lectures.

… an effective theory is an emergent approximation to a deeper theory. A kind of approximation that is specific, reliable, and well controlled— all due to the power of quantum field theory. Given some physical system, there are some things you care about, and some you don’t. An effective theory is one that models only those features of the system that you care about. The features you don’t care about are too small to be noticed, or moving back and forth in ways that everything just averages out. An effective theory describes the macroscopic features that emerge out of a more comprehensive microscopic description. — Carroll, Sean (2016-05-10). The Big Picture: On the Origins of Life, Meaning, and the Universe Itself (pp. 186-187). Penguin Publishing Group. Kindle Edition.

In the macro world, a common example is when we talk about air as a gas (rather than a bunch of molecules) with properties like temperature and pressure. Another example is the concept of center of mass in Newtonian calculations of planetary motion.

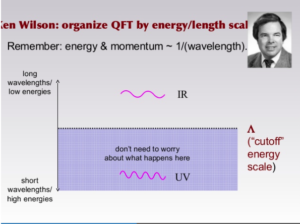
A particular example that Carroll uses is based on the work of American theoretical physicist Kenneth Wilson and How Quantum Field Theory Becomes ‘Effective’ (blog post 6/20/2013).

… Wilson says, quantum field theory comes automatically equipped with a very natural way to create effective theories: keep track of only the long-wavelength/ low-energy vibrations in the fields. … Effective field theories capture the low-energy behavior of the world, and by particle-physics standards, everything we see in our daily lives is happening at low energies. [Theory of Some Low-Energy Things]

The microscopic theory has quarks; the effective theory has protons and neutrons. It’s an example of emergence: the vocabulary we use to talk about fluids is completely different from that of molecules, even though they can both refer to the same physical system. — Carroll, Sean (2016-05-10). The Big Picture: On the Origins of Life, Meaning, and the Universe Itself (p. 188). Penguin Publishing Group. Kindle Edition.

We can make “confident statements about macroscopic behavior” without referencing any deeper level of reality. A practical handle, not a final model of everything. The domain of applicability limits what we need to consider in an analysis. For example (as noted above), in Newtonian mechanics we can ignore the way in which mass is distributed in planetary objects, such Earth, Mars, Jupiter, Saturn, etc. Imagine calculating the path of a baseball and a water balloon. (Chapter 24 in The Big Picture is a must read.)

The fundamental stuff of reality might be something wholly distinct from anything any living physicist has ever imagined; in our everyday world, physics will still work according to the rules of quantum field theory. … It’s this special feature of quantum field theory that gives us the confidence to make such audacious claims about the scope of our knowledge. — Carroll, Sean (2016-05-10). The Big Picture: On the Origins of Life, Meaning, and the Universe Itself (p. 189, 191). Penguin Publishing Group. Kindle Edition.

Here’s a slide that he uses in his lectures about QFT.

 

[1] Witness even the Newtonian computational challenges dramatized in the movie Hidden Figures about NASA’s Project Mercury and other missions in the 1960’s.

[2] We had (at the time) an IBM 360 mainframe and keypunch card system. Grad students would bring in their decks of cards and submit their jobs, and my role was to help them when things went wrong. But the main role for me was not technical (about programming their jobs). The main problem was that they didn’t get the results that they expected.

Grads students, particularly in the social sciences, were trying to prove some relationship, some hypothesis. For example, some conclusion about why people behaved the way they did. Or some conclusion that something caused something else. So that behavioral predictions were possible or mitigation might be applied to a situation. All very fascinating stuff.

Year and year the students would struggle with such things, trying to prove their proposition or hypothesis. They used statistical analysis techniques on collected data. Classical statistical techniques or biomedical statistical packages. Two primary analyses were correlation and regression. Correlations helped establish a relationship (whether there was or not) between inputs and outputs of the study. Today we see such claims all the time on TV. For example, that a certain diet will reduce incidence of a certain disease.

Regression analysis helped determine which factors were really important in the model under study. Certain factors were more important than others. Certain factors might not even be worth collecting data for. That can be tricky. The goal is to use factors that are independent of each other. Lack of independence may mean that you’re really just spending time and money trying the collect sort of the same thing.

Finally, you had to consider how precise the results should be calculated or even presented. If people do X and there’s a relationship to Y, should you say that there’s a 55% correlation or 56% or 55.55%.

And behind all this effort was a basic potential problem about the original data. First there’s GIGO — garbage in, garbage out. And also margin of error for things that were quantifiable or varied with which team member collected the data or due to some other bias in the sampling itself. We see these issues with political polls, for example. Random polls, of course.

[3] Problem solving strategies emphasized when I was teaching math.

• Make an organized list or table
• Use logical reasoning
• Solve a simpler or similar problem (or break into simpler problems or steps)
• Identify too much or too little information (eliminate unnecessary information)
• Look for a pattern
• Make a model or use objects
• Work backwards
• Draw a picture or diagram
• Guess and check
• Simulate a problem (or act it out)
• Use multiple strategies
• Write an equation